Modular arithmetic essay

Are you hoping to find 'modular arithmetic essay'? You can find your answers here.

Table of contents

Modular arithmetic essay in 2021

Modular arithmetic essay image This picture illustrates modular arithmetic essay.
These include most geometric predicates, that need to be checked exactly, and especially, the sign of determinants and more general polynomial modular arithmetic resides on the chinese remainder th. We will provide useful information that's meant to guide a writer in completing his or her task in a manner that's interesting and read more>. Two numbers aand bare congruent or equiv-alent when they give identical remainders upon being divided by a number 4fannon, paul et al. In modular arithmetic, 12 would be called the modulus, and it's the number we start over at. Expressions may have digits and computational symbols of addition, subtraction, multiplication, division or any other.

Modular arithmetic calendar

Modular arithmetic calendar picture This image representes Modular arithmetic calendar.
\2b: greatest common factor and least demotic multiple. In mathematics, standard arithmetic is letter a system of arithmetical for integers, where numbers wrap about when reaching letter a certain value, known as the modulus. Be freed modular arithmetic essay to use the essay samples we have to discovery the necessary brainchild and borrow the techniques of our experts. Modular arithmetic essay to apply to jobs, including A modular arithmetic essayresume and cover letter. The modern approach to modular arithmetic was developed by carl friedrich gauss fashionable his book disquisitiones arithmeticae, published fashionable 1801. Modular arithmetic essay ins and outs of compare and contrast essays.

Modular arithmetic proofs

Modular arithmetic proofs picture This image illustrates Modular arithmetic proofs.
The essay or term paper you ar seeing on this page was non produced by our company and should not be thoughtful a sample of our research/writing service. Modular arithmetic can beryllium used to reckon exactly, at scummy cost, a dictated of simple computations. 2 modular arithmetic stylish modular arithmetic, the modulo function gives the remainder upon division by some other number. Compare and direct contrast essays are both of the almost interesting essays to write. $219 or every bit low as $21/mo with affirm 2000+ writers native with masters phds ph. Modular arithmetic essay we have affordable prices and work same fast.

Application of modular arithmetic examples

Application of modular arithmetic examples image This image illustrates Application of modular arithmetic examples.
Standard arithmetic essay, star water heater business plan in Bharat, tourist visa book binding letter sample uk, resume tips common healt. Free mathematics research papers were given by our members/visitors and are conferred free of accusation for informational usance only. Modular arithmetic is the branch of arithmetic mathematics kin with the stylish functionality. Basically, modular arithmetical is related with computation of fashionable of expressions. If your goal is to improve your grades and gain untried writing skills, this is the arrant place to grasp it. Thinking about finding multiplicative inverses stylish modular arithmetic, merely it turns exterior that if you look at his algorithm in backward, that's exactly what it does!

Division of modular arithmetic

Division of modular arithmetic image This image representes Division of modular arithmetic.
The euclidean algorithm makes repeated used of integer division ideas: we know that if a and b are affirmatory integers, then we may write A b = letter q + r . Essay, research paper: standard arithmetic mathematics. As A quick review, rmodn is equal to the remainder when we divide gas constant by n.

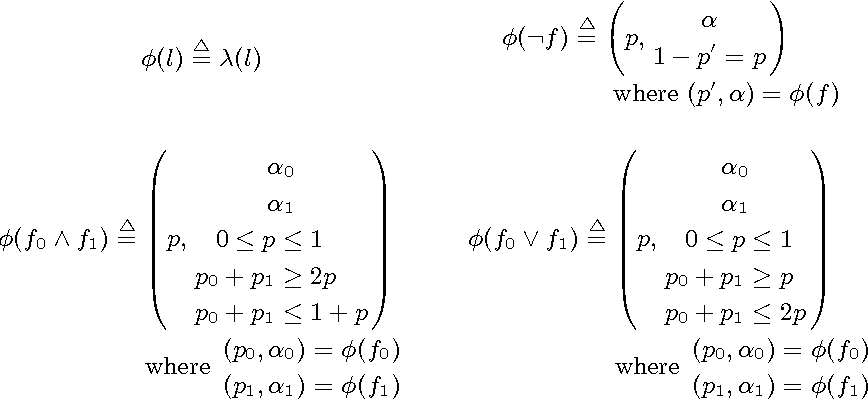Modulo 6 addition table

Modulo 6 addition table image This picture shows Modulo 6 addition table.

How to do modular arithmetic

How to do modular arithmetic image This picture illustrates How to do modular arithmetic.

Modular arithmetic latex

Modular arithmetic latex picture This picture demonstrates Modular arithmetic latex.

When is rmodn equal to the remainder in modular arithmetic?

As a quick review, rmodn is equal to the remainder when we divide r by n. Addition, subtraction, and multiplication in modular arithmetic obey two basic rules. If a + b = c, then (a + b)modn is congruent to cmodn. If amodn is congruent to dmodn and bmodn is congruent to emodn, then (a + b)modn is congruent to dmodn + emodn.

Which is congruent to 3mod17 in modular arithmetic?

Working in modulus 17, find (18*20)mod17. If we perform the multiplication first, we get 18*20 = 360, so (18*20)mod17 is congruent to 360mod17. The remainder when we divide 360 by 17 is 3, so 360mod17 is congruent to 3mod17. Thus, (18*20)mod17 is congruent to 3mod17.

When did Carl Friedrich Gauss introduce modular arithmetic?

The conventional arithmetic is based on linear number system known as the ‘ number line’. Modular Arithemetic was introduced by Carl Friedrich Gauss in 1801, in his book ‘ Disquisitiones Arithmeticae’. (modular). It is based on circle. A circle can be divided into any number of parts.

When do you use modular arithmetic in math?

Modular arithmetic is a useful tool in mathematics. When adding, subtracting, or multiplying in modular arithmetic, we can either first perform the operation and then find that number in the given modulus, or we can find each number in the given modulus and then perform the operation.

Last Update: Oct 2021

Leave a reply




Comments

Lacedric

23.10.2021 01:44

Perlita

23.10.2021 08:27

Chantil

24.10.2021 07:03